MAGNITUDES PROPORCIONALES
TEMAS Y SUBTEMAS:
UNIDAD I.
MAGNITUDES PROPORCIONALES.
1.1 Regla de tres.
¿Qué es la regla de 3 simple?
La regla de 3 simple es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa.
Para hacer una regla de tres simple necesitamos 3 datos: dos magnitudes proporcionales entre sí, y una tercera magnitud. A partir de estos, averiguaremos el cuarto término de la proporcionalidad.
Regla de 3 simple directa
Empezaremos viendo cómo aplicarla en casos de proporcionalidad directa (cuando aumenta una magnitud también lo hace la otra).
Colocaremos en una tabla los 3 datos (a los que llamamos “a”, “b” y “c”) y la incógnita, es decir, el dato que queremos averiguar (que llamaremos “x”). Después, aplicaremos la siguiente fórmula:
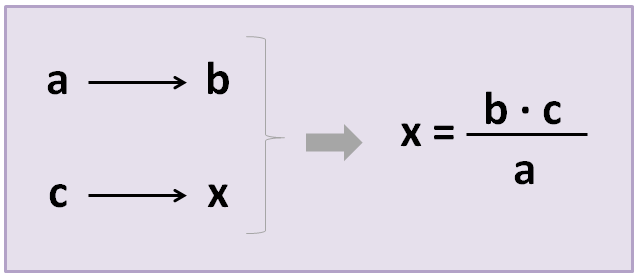
Problema de regla de 3 simple directa
Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos han dicho que 5 centímetros del mapa representan 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?
Vamos a hacer la tabla con los 3 datos y la incógnita (“x”), y hallaremos “x” con la fórmula que acabamos de aprender:
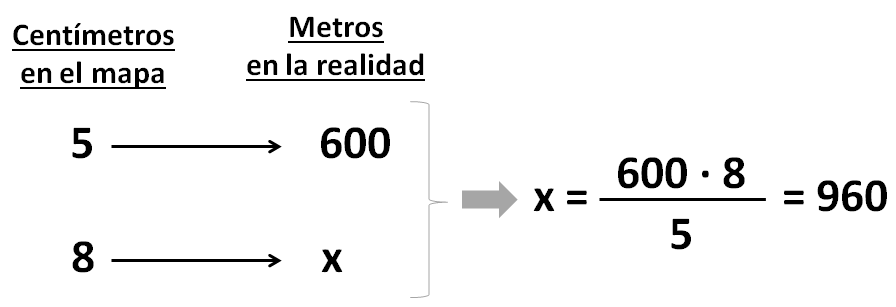
Solución: El parque se encuentra a 960 metros del hotel
Regla de 3 simple inversa
Ahora vamos a ver cómo aplicar la regla de 3 simple en casos de proporcionalidad inversa (cuando aumenta una magnitud disminuye la otra).
Colocaremos los 3 datos y la incógnita en la tabla igual que los hemos colocado en el caso anterior. Pero aplicaremos una fórmula distinta:
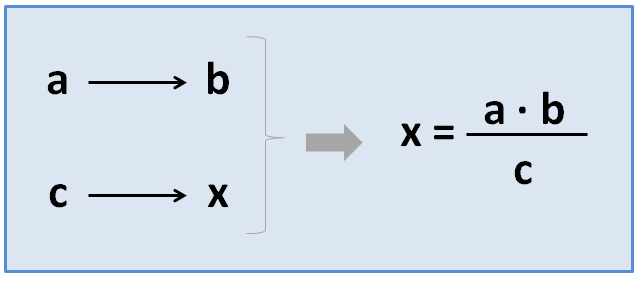
Problema de regla de 3 simple inversa
Vamos a ver un ejemplo con el mismo problema que resolvimos en el post de la semana anterior.
Ayer 2 camiones transportaron una mercancía desde el puerto hasta el almacén. Hoy 3 camiones, iguales a los de ayer, tendrán que hacer 6 viajes para transportar la misma cantidad de mercancía del almacén al centro comercial. ¿Cuántos viajes tuvieron que hacer ayer los camiones?
Colocamos los datos en una tabla y aplicamos la fórmula de la regla de 3 simple inversa:
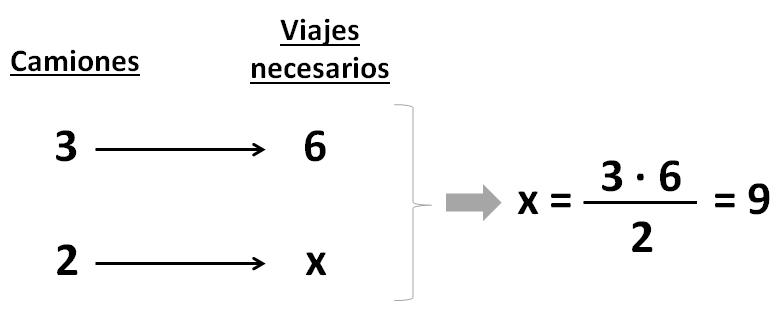
Solución: Ayer los 2 camiones hicieron 9 viajes.
1.2 Tanto por ciento.
El tanto por ciento es una forma de expresar un número como una fracción de 100 (que significa “de
cada 100”), es decir, es una cantidad que corresponde proporcionalmente a una parte de cien. En diversas actividades de la vida cotidiana se aplica la comparación entre números. Para facilitar la
comparación muchos datos numéricos se relacionan en la práctica con el número 100.
Cálculo del Tanto por ciento
Para calcular el Tanto por ciento de un número se multiplica el número por el Tanto por ciento (expresado como como una división de divisor 100 o en notación decimal corriendo la coma dos lugares
a la izquierda)
Por ejemplo (4) Para calcular el 3% de 45 se multiplica 45 por 3/100 (que es lo mismo que 3/100*45) o se multiplica 45 por 0,03, lo que matemáticamente se expresa así: 459*3/10020=9*3/20=27/20=1,35 o 45*0,03 =
1,35. De ambas vías se obtiene que el 3% de 45 es 1,35; lo que es lo mismo que: 1,35 es el 3% de 45.
1.3 Interés.
El interés es el precio que se paga por el uso del préstamo de dinero. Generalmente se expresa como un porcentaje anual sobre la suma prestada por parte de una institución financiera.
Este es visto como una ganancia que obtiene la entidad financiera al momento de otorgar créditos, siendo de alguna manera una recompensa por prestar. En sí, es el porcentaje que el cliente tiene que pagar por obtener un préstamo de dinero.
La cantidad se fija con base en las tasas impuestas por los bancos centrales de cada país, dependiendo de la seguridad de inversión que muestra cada economía y el reflejo del riesgo que tiene cada país. En México, la tasa del banco central es la de Interés Interbancario de Equilibrio (TIIE), la cual se suma al interés que pueda poner un banco sobre cierto producto, ya sea tarjeta de crédito o hipoteca. Sirve para terminar la ganancia que la financiera tendrá o para protegerse en caso de que el cliente no pague el préstamo.
¿Interés simple o compuesto?
Cuando una persona toma prestado dinero de un prestamista o de cualquier banco o institución financiera, la entidad crediticia cobra una cantidad adicional por el uso del dinero, llamado interés. El tipo de interés es pactado mutuamente por ambas partes, y se puede cobrar de dos formas: interés simple o interés compuesto.
El primero es el tipo de interés en el que se cobra solo sobre la cantidad prestada, pero en el caso del interés compuesto, lo que se cobra se calcula sobre la cantidad prestada más el interés acumulado al capital.
Es decir, cada vez que el interés vence para el pago, se agrega al principal, en el cual se calcula el interés para el período siguiente, esto se conoce como interés compuesto.
El interés simple se calcula sobre la cantidad principal, u original, de un préstamo.
El interés compuesto se calcula sobre la cantidad del principal y también sobre el interés acumulado de períodos anteriores y, por lo tanto, puede considerarse como «interés sobre intereses».
Puede haber una gran diferencia en la cantidad de intereses pagaderos sobre un préstamo si los intereses se calculan de forma compuesta en lugar de simple. En el lado positivo, la magia de la capitalización compuesta puede ser una ventaja para tus inversiones y puede ser un factor potente en la creación de riqueza.
Si bien el interés simple y el interés compuesto son conceptos financieros básicos, familiarizarse completamente con ellos puede ayudarte a tomar mejores decisiones cuando solicites un préstamo o decidas invertir en productos financieros como los depósitos bancarios.
Si, por ejemplo, estás pensando en pedir un préstamo, lo aconsejable es tener en cuenta primero el coste que puede tener para ti el solicitarlo. Si vas a pedir un préstamo, lo normal es que optes por aquellas entidades que te impongan unas tasas de interés más bajas. Sin embargo, desde el punto de vista de los inversores, una tasa alta será más beneficiosa.
Tanto el interés simple como el interés compuesto son opciones populares en el mercado, pero ¿sabes bien cuáles son sus diferencias? Te las detallamos para que puedas conocer mucho mejor estos conceptos financieros.
1.4 Descuento.
En el ámbito de la economía financiera, descuento es una operación que se lleva a cabo en instituciones bancarias en las que éstas adquieren pagarés o letras de cambio de cuyo valor nominal se descuenta el equivalente a los intereses que generaría el papel entre su fecha de emisión y la fecha de vencimiento.
Descuento
- El descuento legal o racional. En el descuento racional, el descuento se calcula aplicando el tipo de interés y las leyes del interés simple, mientras que en el comercial, el descuento se calcula sobre el valor nominal del documento.
-
-
{\displaystyle D={\frac {N\cdot i\cdot t}{1+i\cdot
t}}}
-
{\displaystyle D={\frac {N\cdot i\cdot t}{1+i\cdot
t}}}
- Descuento de los Títulos de Créditos comerciales
Es la adquisición, por parte del descontador, de un crédito a cargo de un tercero, de que es titular el descontatario, mediante el pago al contado del importe del crédito, menos la tasa del descuento.
Se calculan utilizando la fórmula:
-
-
{\displaystyle D=N\cdot d\cdot t}
-
{\displaystyle D=N\cdot d\cdot t}
Donde:
- D es igual al descuento efectuado
- N es el valor nominal del documento
- i representa la tasa de interés del descuento
- d representa la tasa de descuento aplicada
- t representa el tiempo.
1.5 Repartimientos proporcionales.
Reparto es el acto y el efecto de repartir (proceder a la distribución de algo que se divide en fragmentos o que se envía a diferentes lugares). Proporcional, por su parte, es aquello vinculado a una proporción (la correspondencia que existe en los componentes de un todo).
Debido a que la proporcionalidad es la razón que se registra entre magnitudes, el reparto proporcional consiste en la distribución de una cantidad en partes proporcionales. En otras palabras: el reparto proporcional implica repartir una magnitud total de manera proporcional entre diversas magnitudes de una misma clase.
Supongamos que un padre quiere entregar una mensualidad a sus hijos que resulte proporcional a sus edades. El hombre dispone de 500 pesos por mes que repartirá entre los niños de 10, 12 y 14 años de edad. Tendremos, entonces, tres cantidades: a (la cantidad que corresponde al niño de 10 años), b (cantidad para el niño de 12) y c (cantidad para le niño de 14). Cada una de estas cantidades debe dividirse por la edad correspondiente:
a / 10 = b / 12 = c / 14
La propiedad de las razones iguales nos indica que:
a+ b + c / 10 + 12 + 14
Como a + b + c es el total del dinero que se repartirá (500 pesos):
500 / 36
a / 10 = 500 / 36
b / 12 = 500 / 36
c / 14 = 500 / 36
a = 138,8 (139 pesos)
b = 166,6 (167 pesos)
c = 194,4 (194 pesos)
Es importante conocer que existen dos tipos fundamentales de repartos proporcionales, como así queda claro en el ámbito de las matemáticas. Así, por un lado, está el llamado directo, que es que se basa en el hecho de que a mayor cantidad corresponde, por tanto, mayor proporción.
Para poder entender este podemos establecer un ejemplo claro. Imaginemos que tres personas deciden poner en marcha un negocio juntas y cada una aporta una cantidad concreta como inversión para que la misma pueda llevarse a cabo: Mariana pone 5.000 euros, Luis invierte 8.000 euros y Sara decide aportar 10.000 euros.
Pasado un año los tres socios deciden sentarse y comprobar las cuentas de esos primeros doce meses. Al hacerlo descubren que han obtenido unos beneficios de 2.300 euros que, por tanto, deberán repartirse de manera proporcional a lo que han invertido. Es decir, que la que más recibirá, porque es la que más dinero puso, será Sara, después le seguirá Luis y finalmente Mariana.
Si realizáramos el correspondiente cálculo descubriríamos que, de esos 2.300 euros, Sara se llevaría 1.000 euros, Luis 800 y Mariana 500 euros.
Por otro lado, nos encontramos con el reparto proporcional inverso, que parte de la máxima de que a más cantidad, menor proporción.
No obstante, no podemos pasar por alto que también existe lo que se conoce como reparto proporcional compuesto que es aquel que tiene lugar cuando las partes que se van a repartir son proporcionales al producto de varios números. A su vez, ese puede ser directo, inverso o mixto.


