UNIDAD IV, V y VI
UNIDAD IV. DESCRIPCIÓN DE DATOS DE NEGOCIOS: MEDIDAS DE VARIABILIDAD.
4.1 Medidas de variabilidad en conjunto de datos.
Las medidas de variabilidad, también llamadas medidas de dispersión, son estadísticas que cuantifican la variabilidad de un conjunto de datos. Permiten determinar la confiabilidad de una medida de resumen de un conjunto de datos.
Algunas de las medidas de variabilidad más utilizadas son: Rango: La diferencia entre el valor máximo y el mínimo del conjunto de datos, Rango intercuartílico, Varianza, Desviación estándar, Coeficiente de variación.
La variabilidad es el grado en que los puntos de datos de un conjunto de datos se diferencian entre sí y del valor promedio. Las medidas de variabilidad indican si las puntuaciones de una variable están muy alejadas de la media.
El Coeficiente de Variación de Pearson (CV) es una medida que se utiliza para comparar la variabilidad relativa entre variables con diferentes unidades de medida.
4.2 El Rango.
El rango es un valor numérico que indica la diferencia entre el valor máximo y el mínimo de una serie de datos o muestra estadística.
- El rango es la diferencia entre el valor más alto y el más bajo en un conjunto de datos, mostrando cuánto varían los valores.
- El rango puede cambiar con nuevos datos, reflejando variaciones o tendencias emergentes.
- Es especialmente útil en finanzas y economía para evaluar la variabilidad o dispersión en el valor de activos, productos, o indicadores económicos.
El rango, en términos estadísticos, es una medida que nos ayuda a entender cuán dispersos o variados son los datos dentro de un conjunto. Para calcularlo, simplemente restamos el valor más pequeño del conjunto del valor más grande. Esta resta nos da una cifra que representa la distancia total entre estos dos extremos.
Por ejemplo, si analizamos los ingresos en un grupo de personas y encontramos que el menor ingreso es de 10 euros y el mayor de 100 euros, el rango de ingresos en este grupo es de 90 euros. Esto nos da una idea rápida de la variabilidad de los ingresos dentro del grupo.
4.3 Rangos Modificados.
Los rangos modificados son rangos que se construyen eliminando algunos de los valores extremos de las porciones finales de una distribución.
El rango de variación es un número que indica la distancia entre el valor mínimo y el valor máximo de una población estadística. Se calcula con base en diferentes factores.
Para calcular el rango de una muestra o población, se utiliza la fórmula: rango = valor máximo - valor mínimo.
El rango, la varianza y la desviación estándar son medidas de dispersión que se utilizan en la estadística descriptiva para describir la dispersión de los valores de una muestra
4.4 La desviación Media.
Desviación media: Qué es, fórmula y cómo calcularla
desviación media
En estadística, la desviación media es una medida importante de dispersión que nos permite entender cuánto varían los datos de un conjunto promedio.
La desviación es una herramienta fundamental para analizar y comprender conjuntos de datos en diversas disciplinas, como la economía, la psicología, la medicina y muchas otras.
Comprender cómo calcular y utilizarla es crucial para poder hacer afirmaciones precisas y tomar decisiones basadas en datos. En este artículo, explicaremos qué es, cómo se calcula y por qué es importante en el análisis de datos.
¿Qué es la desviación media?
La desviación media es una medida que se utiliza para entender qué tanto se alejan los datos de un conjunto promedio.
Es una medida que nos ayuda a entender cuánto varían los datos de un conjunto promedio. Si la desviación es grande, significa que los datos están muy dispersos o variados, mientras que si es pequeña, significa que los datos están muy cercanos entre sí.
Fórmula para calcular la desviación media
La fórmula sencilla para calcularla es la siguiente:
Desviación media = Σ | Xi – X | / N
Donde:
Σ = Suma de los términos
| Xi – X | = Valor absoluto de la diferencia entre cada dato y la media
X = Media del conjunto de datos
N = Número de datos en el conjunto
En palabras sencillas, para calcular la desviación, se suman las diferencias absolutas entre cada valor del conjunto de datos y su media, y se divide el resultado entre el número total de datos. Esta fórmula nos da una medida de dispersión promedio de los datos del conjunto en relación a su media.
4.5 La varianza y la desviación estándar
La varianza y la desviación estándar son medidas que proporcionan información similar sobre la dispersión de datos, pero con algunas diferencias:
Definición
La varianza es la desviación estándar al cuadrado, y la desviación estándar es la raíz cuadrada de la varianza.
Unidad de medida
La desviación estándar se expresa en las mismas unidades de medida que los datos originales.
Interpretación
La varianza mide la distancia media al cuadrado respecto a la media, mientras que la desviación estándar mide la distancia media respecto a la media.
Cálculo
La varianza es necesaria para calcular la covarianza y algunas matrices econométricas.
Símbolo
La varianza se representa con los símbolos σ2 y S2. σ2 se refiere a la varianza de una población, mientras que S2 se refiere a la varianza de una muestra.
La varianza y la desviación estándar indican si los valores están más o menos próximos a las medidas de posición. Cuanto mayor sea la varianza, mayor será la dispersión de los valores y menor representatividad tendrá la media aritmética. Si no hubiera ninguna variación en los datos, la desviación estándar sería cero.
4.6 Cálculos abreviados de la Varianza y la desviación estándar
Los símbolos para abreviar la varianza y la desviación estándar son:
Varianza
Se utiliza el símbolo σ2 para representar la varianza de una población y S2 para representar la varianza de una muestra.
Desviación estándar
Se utiliza el símbolo σ para representar la desviación estándar de una población y s para representar la desviación estándar de una muestra.
La varianza es el promedio de las distancias al cuadrado entre las observaciones y la media. La desviación estándar es la raíz cuadrada de la varianza.
4.7 Uso de la desviación estándar
La desviación estándar es un número que se usa para medir la dispersión de un conjunto de datos y se utiliza en diversas áreas, como la investigación, las finanzas y la metodología six sigma:
Investigación
Se utiliza para resumir datos continuos, junto con la media. Es adecuada cuando los datos no están sesgados o tienen valores atípicos.
Finanzas
Se utiliza para calcular la volatilidad histórica de un activo financiero. Se calcula a partir de los precios históricos del activo. Una mayor desviación estándar indica mayor volatilidad.
Metodología six sigma
Se utiliza para dar forma a las distribuciones de probabilidad, como la distribución normal.
La desviación estándar es la raíz cuadrada del promedio de las distancias al cuadrado que van desde las observaciones a la media
https://www.youtube.com/watch?v=dEcJmDT8wBg
4.8 El coeficiente de Variación.
El coeficiente de variación, también denominado como coeficiente de variación de Pearson, es una medida estadística que nos informa acerca de la dispersión relativa de un conjunto de datos.
Puntos clave
Es útil para comparar la variabilidad entre diferentes series de datos, incluso si sus unidades de medida no son las mismas.
Un coeficiente de variación bajo indica que los datos están más uniformemente distribuidos alrededor del promedio, mientras que un valor alto señala una mayor dispersión.
4.9 Coeficiente de Asimetría de Pearson.
El coeficiente de asimetría de Pearson es una medida estadística que cuantifica el nivel y la dirección de la asimetría de una distribución. Se calcula a partir de la diferencia entre la media aritmética, la mediana y la moda. El resultado se normaliza dividiendo entre la desviación típica.
El coeficiente de asimetría de Pearson se puede utilizar en distribuciones: Unimodales, Uniformes, Moderadamente asimétricas.
El coeficiente de asimetría caracteriza el grado de asimetría de una distribución en relación a su media. Los resultados pueden ser:
Asimetría positiva, que indica una distribución unilateral que se extiende hacia valores más positivos
Asimetría negativa, que indica una distribución unilateral que se extiende hacia valores más negativos
Para entender la simetría y la asimetría de una variable, se puede considerar que:
Una distribución es simétrica si la dispersión de los datos es equitativa a ambos lados del centro
Una distribución es asimétrica si la dispersión es diferente a un lado que a otro
El eje de simetría es una recta paralela al eje de ordenadas que pasa por la media de la distribución
https://www.youtube.com/watch?v=reAULQ3dW60
4.10 El Rango y los Rangos modificados para datos agrupados.
El rango es una medida de dispersión que indica la diferencia entre el valor más grande y el valor más pequeño de una serie de datos. Se utiliza para obtener una idea de la dispersión de los datos, es decir, qué tanto se agrupan o dispersan con respecto a su media aritmética.
La fórmula para calcular el rango es:
Rango = valor máximo de la muestra - valor mínimo de la muestra
Por ejemplo, si la altura de 7 personas es de 1.90 m y 1.50 m, el rango se calcula como 1.90 m - 1.50 m = 0.4 m.
El rango puede presentar fallas como medida de dispersión cuando: Hay medias desproporcionadas, Se realiza un muestreo aleatorio, Los datos provienen de una muestra y no de una población, Hay datos atípicos.
Un rango modificado es un rango que se obtiene al eliminar algunos valores extremos de las porciones finales de una distribución. Algunos ejemplos de rangos modificados son el 50% central, el 80% central, el 90% central y el 95% central.
El rango, también conocido como span, es una medida de dispersión que se calcula como la diferencia entre el valor más grande y el más pequeño de una distribución. Un rango mayor indica que los datos están más dispersos.
Para agrupar datos, se utilizan intervalos de igual amplitud denominados clases. Esto se hace cuando las variables toman muchos valores o son continuas.
Otras medidas de dispersión para datos agrupados son la varianza, la desviación estándar y el coeficiente de variación
https://www.youtube.com/watch?v=N59NR844bqs
4.11 La desviación media para datos agrupados.
Fórmulas de la desviación media para datos agrupados

Donde:
- fi: frecuencia absoluta de cada valor, es decir, el número de veces que aparece el valor en el estudio.
- xi: marca de clase. Es el punto medio del límite inferior y el límite superior de cada intervalo.
- k: número de clases.
- D. M.: desviación media.
- x̄: media aritmética de los datos.
En los problemas, seguiremos los siguientes pasos:
- Calculamos las marcas de clase xi.
- Calculamos el número de elementos n.
- Calculamos la media x̄.
- Calculamos la desviación media D.M..
Ejemplo 1:
Calcular la desviación media de las edades indicadas en la tabla de frecuencias:
Desviación-media-para-datos-agrupados-ejercicios resueltos
Solución:
Lo primero que haremos será calcular las marcas de clase xi. Recuerda que la marca de clase es el punto medio del límite inferior y del límite superior de cada intervalo, su fórmula es:
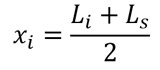
Agregamos una columna más a nuestra tabla para la marca de clase xi:

A continuación, calculamos el número de valores o número de datos “n”, solo tenemos que sumar las frecuencias:


El número de valores es 30.
A continuación, vamos a calcular la media x̄, recordemos su fórmula:

En la tabla, iremos buscando las expresiones que aparecen en la fórmula. Por ello, agregamos una columna más a nuestra tabla, en la cual colocaremos los valores de xi・fi.
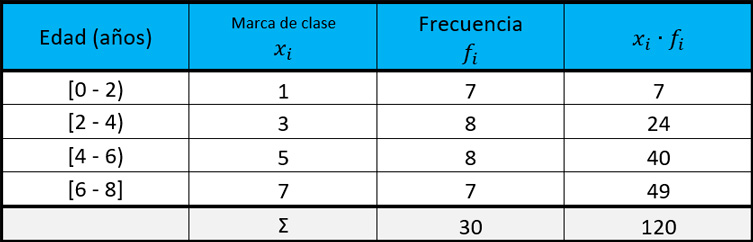
Ahora sí, aplicamos la fórmula:

El valor de la media es de 4 años.
La fórmula de la desviación media para datos agrupados es:

Agregamos 3 columnas más en la tabla de frecuencias:

Aplicamos la fórmula:

El valor de la desviación media es de 1,93 años.
4.12 La Varianza y la desviación estándar para datos agrupados.
https://www.youtube.com/watch?v=zAKZbfqP5MU
4.13 Resultados por Computadora.
UNIDAD V. PROBABILIDAD.
5.1 Definiciones Básicas de Probabilidad.
La probabilidad es un cálculo matemático que mide la posibilidad de que ocurra un evento en circunstancias de azar. Se define como el grado de certeza de que un suceso ocurra o no.
Algunos conceptos básicos de probabilidad son:
La probabilidad de un suceso seguro es 1, mientras que la probabilidad de un suceso imposible es 0.
La probabilidad de cualquier suceso está comprendida entre 0 y 1.
Para obtener la probabilidad de un suceso, se determina la frecuencia con la que ocurre y se realizan cálculos teóricos.
La probabilidad se calcula dividiendo el número de casos favorables entre el total de casos posibles.
La probabilidad se utiliza en diversas ciencias naturales y sociales, ya que permite manejar escenarios posibles. El análisis de los eventos gobernados por la probabilidad se llama estadística.
5.2 Expresión de Probabilidad.
La probabilidad se expresa en porcentaje o en fracciones:
En porcentaje
La fórmula para calcular la probabilidad es: Probabilidad = Casos favorables / Casos posibles x 100.
En fracciones
En el numerador se coloca el número de casos favorables y en el denominador el número total de posibilidades.
La probabilidad es un cálculo matemático que indica la posibilidad de que ocurra un evento en circunstancias aleatorias. El valor de la probabilidad se encuentra entre 0 y 1, donde 0 significa que es imposible que el evento ocurra y 1 significa que es seguro que ocurra.
La probabilidad se relaciona con la estadística, que es el análisis de los eventos gobernados por la probabilidad. La estadística se encarga de recopilar y analizar datos para generar explicaciones y predicciones.
5.3 Eventos mutuamente excluyentes y no excluyentes.
Eventos excluyentes
PROBABILIDAD
Los eventos mutuamente excluyentes son aquellos que si un evento sucede significa que el otro no puede ocurrir.
Ejemplo de evento no excluyente
En probabilidad los eventos mutuamente excluyentes son claves de la probabilidad. La probabilidad es la posibilidad de que un evento ocurra en una determinada cantidad de tiempo
A= Suceso 1
B= Suceso 2
A y B son excluyentes si la intersección de A y B son cero
Ejemplo moneda
A= cara
B= cruz
si sale cara nunca podra salir una cruz y si sale cruz nunca saldrá.
Ejemplo Dado
A= obten 2
B= obten 3
La probabilidad de que salga un 2 o un 3 es igual a 1/6
Sea A el suceso de sacar un As de una baraja de 52 cartas y B sacar una carta con corazón rojo.
las probabilidades que tenemos son:
P (A) = 4/52
P (B) = 13/52
P (A y B) = 1/52
Ejemplo moneda
Al lanzar una moneda es un evento mutuamente excluyente que tiene 50% de probabilidad.
Remplazando los valores en la formula
P (A o B) = P(A) + P(B) - P(A y B)
P (A o B) =4/42 + 13/52+1/52= 4/13
Formula para evento mutuamente excluyente
A continuación vídeo y posteriormente la dinámica
P (A U B)= P(A) + P(B)
Ejemplo:
Sacar un carta de corazones y una carta de espadas, son eventos excluyentes, es decir las cartas o son de corazones o son de espadas.
Formulas
P (A o B) = P (A) = P (B) - P(A y B)
o
P (A U B) = P(A) + P(B) - (A U B)
Eventos no excluyentes
Dos o más eventos son no excluyentes, o conjuntos, cuando es posible que ocurran ambos. Esto no indica que necesariamente deban ocurrir estos eventos en forma simultánea.
Regla de adición
Siendo: P(A) = probabilidad de ocurrencia del evento AP(B) = probabilidad de ocurrencia del evento BP(A y B) = probabilidad de ocurrencia simultanea de los eventos A y B
P(A o B) = P(A) + P(B) ± P(A y B)
si A y B son no excluyentes
Eventos excluyentes y no excluyentes
https://www.youtube.com/watch?v=pRFacUMELPQ
5.4 Las reglas de Adición.
Las reglas de adición en matemáticas son:
Regla de la adición o de la suma
Se aplica cuando los eventos son mutuamente excluyentes, es decir, no pueden ocurrir al mismo tiempo. En este caso, la probabilidad de que ocurra uno u otro evento es igual a la suma de las probabilidades individuales de cada evento.
Ley de los signos de la suma
Se aplica cuando se realizan operaciones de suma con números reales. Las reglas son:
Si los dos números son positivos, se suman y se mantiene el signo «+».
Si los dos números son negativos, se suman y se mantiene el signo «-«.
La adición o suma es una operación matemática que consiste en combinar o añadir dos o más números para obtener un total.
Regla de la adición La regla de la adición o regla de la suma establece que la probabilidad de ocurrencia de cualquier evento en particular es igual a la suma de las probabilidades individuales, si es que los eventos son mutuamente excluyentes, es decir, que dos no pueden ocurrir al mismo tiempo. P(A o B) = P(A) U P(B) = P(A) + P(B) si A y B son mutuamente excluyente. P(A o B) = P(A) + P(B) − P(A y B) si A y Bson no excluyentes. Siendo: P(A) = probabilidad de ocurrencia del evento A. P(B) =probabilidad de ocurrencia del evento B. P(A y B) =probabilidad de ocurrencia simultánea de los eventos A y B.
5.5 Eventos dependientes, eventos Independientes y Probabilidad Condicional.
Dos eventos son independientes si el resultado del segundo evento no es afectado por el resultado del primer evento. Si A y B son eventos independientes, la probabilidad de que ambos eventos ocurran es el producto de las probabilidades de los eventos individuales.
P ( A y B ) = P ( A ) · P ( B )
Ejemplo 1:
Una caja contiene 4 canicas rojas, 3 canicas verdes y 2 canicas azules. Una canica es eliminada de la caja y luego reemplazada. Otra canica se saca de la caja. Cuál es la probabilidad de que la primera canica sea azul y la segunda canica sea verde?
Ya que la primera canica es reemplazada, el tamaño del espacio muestral (9) no cambia de la primera sacada a la segunda así los eventos son independientes.
P (azul luego verde) = P (azul) · P (verde)

Dos eventos son dependientes si el resultado del primer evento afecta el resultado del segundo evento así que la probabilidad es cambiada. En el ejemplo anterior, si la primera canica no es reemplazada, el espacio muestral para el segundo evento cambia y así los eventos son dependientes. La probabilidad de que ambos eventos ocurran es el producto de las probabilidades de los eventos individuales:
P ( A y B ) = P ( A ) · P ( B )
5.6 Las reglas de Multiplicación.
En estadística, la regla de multiplicación se utiliza para calcular la probabilidad de que ocurran dos eventos, multiplicando la probabilidad de cada uno:
Si los eventos son independientes, es decir, no se influyen entre sí, entonces la probabilidad de que ocurran ambos es igual al producto de sus respectivas probabilidades.
Si el primer evento afecta la probabilidad del segundo, se trata de eventos dependientes.
Por ejemplo, si se extraen dos cartas de un paquete sin reemplazar la primera, los dos eventos son dependientes.
El principio de multiplicación, también conocido como principio fundamental de conteo, establece que si un evento puede ocurrir de m maneras y un segundo evento puede ocurrir en n maneras, entonces los dos eventos pueden ocurrir en m × n maneras
5.7 Teorema de Bayes.
El teorema de Bayes, en la teoría de la probabilidad, es una proposición planteada por el matemático inglés Thomas Bayes (1702-1761)1 y publicada póstumamente en 1763,2 que expresa la probabilidad condicional de un evento aleatorio
En términos más generales y menos matemáticos, el teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de una distribución binomial (en terminología moderna). A la muerte de Bayes, su familia transfirió sus documentos a un amigo, el ministro, filósofo y matemático Richard Price.
Teorema de Bayes: Explicación sencilla
Dicho de manera más simple, el teorema de Bayes es una herramienta que nos ayuda a entender mejor cómo la nueva información afecta a la probabilidad de que ocurra algo.
Imagina que tienes una hipótesis o una creencia inicial sobre algo, como la posibilidad de que llueva mañana. Si recibes nueva información, como que el cielo está muy nublado hoy, el teorema de Bayes te permite ajustar la probabilidad de que llueva mañana teniendo en cuenta esta nueva información.
En otras palabras, este teorema nos permite actualizar nuestras creencias o probabilidades sobre un evento (llamémoslo A) después de considerar una nueva evidencia o información (llamémosla B).
A diferencia de otros enfoques que parten de la probabilidad de la nueva evidencia para decir algo sobre el evento original, Bayes trabaja al revés: parte de lo que sabemos sobre el evento original para inferir la nueva probabilidad teniendo en cuenta la nueva evidencia.
Aunque el teorema de Bayes ha sido objeto de críticas, principalmente por malas interpretaciones o aplicaciones incorrectas, cuando se utiliza correctamente (es decir, cuando los eventos son claros y bien definidos), es una herramienta poderosa y válida para el razonamiento probabilístico.
5.8 Tablas de Probabilidades Conjuntas.
Una tabla de probabilidades conjuntas es una distribución de probabilidad que representa dos o más variables aleatorias. En una tabla de contingencia, la probabilidad conjunta de cada celda se calcula dividiendo la frecuencia de esa celda por la frecuencia total de la tabla.
Se define como tabla de probabilidad conjunta a aquella tabla la cual permite y muestra la interacción de dos eventos y las probabilidades de que el resultado entre cualquiera de las variables pase. Se llama de probabilidad conjunta debido a que cada uno de estos valores da la probabilidad de la intersección de dos eventos, las probabilidades se llaman probabilidades conjuntas.Estás nos ayudan concretamente para poder visualizar un problema y poder realizar las probabilidades de dichos eventos, nos proporciona un resumen de la información de estos eventos y probabilidad. De aquí surgen las tablas de contingencia,las cuales se utilizan para clasificar el número de observaciones respecto a dos características o variables.

5.9 Permutaciones.
En estadística, las permutaciones son una función que muestra el número de combinaciones que se pueden obtener para elegir un número determinado de objetos de un grupo, teniendo en cuenta el orden.
Una permutación es una forma de ordenar los elementos de un conjunto, en la que el orden de aparición es importante. Por ejemplo, si se tienen los dígitos 2, 5, 8, se pueden formar los números 258, 285, 528, 582, 825 y 852, cada uno de ellos es una permutación de los dígitos dados.
La fórmula para calcular el número de permutaciones de n elementos tomados de r en r es: \(nfactorial/(n-rfactorial)\). En esta fórmula, \(n\) es el número de elementos del conjunto y \(r\) es el tamaño de los grupos que se forman.
Existen tres tipos de permutaciones: lineal, circular y con elementos repetidos.
https://www.youtube.com/watch?v=_OyZ7azgF7U
5.10 Combinaciones.
En estadística, una combinación es una técnica de conteo que permite calcular el número de arreglos que se pueden realizar con un conjunto de elementos, sin importar el orden en que se organicen.
Una combinación simple es un subconjunto o agrupamiento de un número determinado de elementos, sin que ninguno se repita. Por ejemplo, si se tiene un conjunto de tres números P, Q y R, la cantidad de formas en que se pueden seleccionar dos números de cada conjunto es una combinación.
La fórmula para calcular combinaciones es: n C r = n! / [r!( n – r)!]
UNIDAD VI. ANÁLISIS DE SERIES DE TIEMPO Y PRONOSTICOS DE NEGOCIOS.
6.1 El Modelo clásico de las series de tiempo.
El modelo clásico de series de tiempo, también conocido como método de descomposición, considera que los datos de una serie de tiempo están compuestos por cuatro patrones básicos: Tendencia, Variaciones estacionales, Variaciones cíclicas, Variaciones residuales.
Estos patrones se pueden plantear en términos de una relación multiplicativa, aditiva o mixta.
Una serie de tiempo es una colección de observaciones sobre un fenómeno que se realizan en momentos sucesivos del tiempo. El análisis de series de tiempo es una técnica estadística que se utiliza para extraer estadísticas significativas y otras características de los datos.
Los pronósticos son un método que se utiliza para predecir una variable de respuesta, como ganancias mensuales, comportamiento de acciones o cifras de desempleo. Los pronósticos se basan en patrones de datos existentes.
6.2 Análisis de tendencia.
El análisis de tendencias es un método que consiste en estudiar datos para identificar patrones y tendencias que permitan tomar decisiones. Se puede aplicar en diferentes ámbitos, como en finanzas, marketing, I+D, empresas de tecnología, entre otros.
El análisis de tendencias puede ayudar a:
Identificar cambios significativos en el Balance general y el Estado de resultados
Analizar el rendimiento de un valor concreto, como una acción o un bono
Comprender la situación del mercado y los hábitos de los consumidores
Predecir la relevancia de un nuevo producto para el público objetivo
Obtener información valiosa sobre las preferencias de los consumidores, el panorama competitivo y las oportunidades emergentes
Para realizar un análisis de tendencias de manera eficaz, es importante: Comenzar con objetivos manejables, Utilizar las herramientas adecuadas, Comprender el contexto analítico, Interpretar los resultados de forma objetiva.
Una tendencia es un cambio gradual ascendente o descendente en el nivel de la serie o la trayectoria que siguen los valores de la serie.
https://www.youtube.com/watch?v=n6YjVGtSrRk
6.1 Análisis de variaciones Cíclicas.
El análisis de variaciones cíclicas es una técnica que se utiliza para estudiar los altibajos que se repiten en un período de tiempo, y que se deben al ciclo económico.
Las variaciones cíclicas son oscilaciones periódicas que se producen con una frecuencia superior a un año. Suelen deberse a la alternancia de etapas de prosperidad económica (crestas) con etapas de depresión (valles).
Para calcular la variación cíclica se pueden seguir los siguientes pasos:
Estimar la tendencia (T) y los valores estacionales (S) de la serie de tiempo.
Dividir los valores de la serie de tiempo (Y) por la tendencia (T) y el valor estacional estimado (S).
Obtener el componente cíclico (C) y aleatorio (R).
En epidemiología, las variaciones cíclicas son variaciones que se producen en un lapso de varios años y ocurren en algunas enfermedades infecciosas como el sarampión, la meningitis, etc.
6.2 Medición de las Variaciones Estacionales.
La variación estacional se puede medir mediante el índice de variación estacional, que se calcula promediando el cociente entre la serie original y la serie de medias móviles.
Para calcular el factor de estacionalidad de un mes, se dividen las ventas mensuales por las ventas totales del año. El factor de estacionalidad es un índice que indica cuánto más o menos se vende en un periodo concreto respecto al promedio anual, semanal o diario.
La variación estacional es la variación que se produce en una serie temporal a lo largo de un año y que se repite con más o menos regularidad. Puede ser causada por la temperatura, las precipitaciones, los días festivos, los ciclos de estaciones o los días festivos.
El período estacional es el tiempo entre un "pico" y otro en una serie de datos.
6.3 Aplicación de Ajustes Estacionales.
¿Porqué desestacionalizar una serie?
1.- La comparación entre meses o trimestres de diferentes años, necesitan que las series no contengan distorsiones estacionales, que pueden inducir a errores en la toma de decisiones.
2.- Las series desestacionalizadas permiten analizar la evolución de la serie año tras año.
3.- Permiten un mejor análisis
Objetivo
El objetivo de los ajustes estacionales es eliminar efectos estacionales con el objetivo de analizar la tendencia de una serie temporal y hacer comparaciones de la serie entre momentos arbitrarios, habiendo compensado los efectos estacionales.
Por ejemplo en la tasa de desempleo, ya que se conoce que las estaciones del año tienen impactos diferentes sobre la actividad económica.
Es decir, elimina los factores estacionales que influyen en el comportamiento de las estadísticas económicas.
A estos datos ajustados se les llama datos ajustados estacionalmente o datos desestacionalizados.
El componente estacional corresponde a los efectos periódicos que se repiten cada año, aproximadamente en las mismas fechas y con la misma magnitud y cuyas causas pueden considerarse ajenas a la naturaleza económica de las series, como pueden ser ciertas festividades fijas, el clima, las vacaciones, etc.
6.4 Pronósticos basados en los factores de tendencia y Estacionales.
Los pronósticos basados en factores de tendencia y estacionales se realizan a partir de datos históricos para predecir la demanda futura:
Pronóstico estacional: Utiliza datos históricos de temporadas, como ventas reales, para pronosticar la demanda de temporadas futuras. Los pronósticos estacionales pueden ser mensuales, trimestrales, por evento, y más.
Pronóstico de tendencia: Brinda una visión panorámica del negocio, lo que permite anticipar cambios y adaptarse a nuevas condiciones.
Tendencia: Es el comportamiento o movimiento suave de la serie a largo plazo.
Estacionalidad: Son los movimientos de oscilación dentro del año.
Para aplicar un índice de estacionalidad, se multiplica el pronóstico desestacionalizado para un mes por el índice para ese mes. Por ejemplo, si el pronóstico desestacionalizado es de 1000 unidades para un mes con un índice de estacionalidad de 0,90, el pronóstico ajustado estacionalmente será de 900 unidades para ese mes.
Los métodos de serie de tiempo descubren un patrón en los datos históricos y lo extrapolan hacia el futuro.
6.5 Pronósticos cíclicos e indicadores de Negocios.
Los pronósticos y los indicadores económicos son herramientas que se utilizan para predecir ciclos económicos y planear negocios:
Pronósticos
Son estimaciones del comportamiento futuro de una empresa, basadas en el análisis de datos, el estudio de audiencias y las condiciones de la industria. Los pronósticos son una herramienta útil para la planeación de las empresas, ya que permiten definir metas reales o establecer estrategias para alcanzar metas retadoras.
Indicadores económicos
Son medidas que permiten predecir el inicio de un ciclo económico o anticipar la dirección de la economía. Los indicadores económicos se pueden clasificar en adelantados, rezagados y coincidentes. Los indicadores coincidentes son la medida más en tiempo real del ciclo económico. Algunos ejemplos de indicadores adelantados son:
Horas de trabajo semanales promedio en la industria manufacturera
Pedidos de bienes a las fábricas
Permisos de construcción de viviendas
Precios de las acciones
Para pronosticar los ciclos económicos se utilizan métodos como el análisis de series temporales y los modelos econométricos. Los métodos de series de tiempo son adecuados para la predicción a corto plazo, ya que se basan en la demanda histórica.
6.6 La suavización exponencial como método de pronóstico.
La suavización exponencial es un método de pronóstico que se utiliza para estimar la demanda de un producto o para predecir series temporales. Se basa en la idea de que la demanda será similar a la media de los consumos históricos, pero dando más peso a los valores más recientes.
Es uno de los métodos de predicción más antiguos y estudiados. Se puede utilizar en situaciones donde los valores de las series temporales siguen una tendencia gradual o tienen un comportamiento estacional.
Para realizar un pronóstico con el método de suavización exponencial, se pueden seguir los siguientes pasos:
Recopilar datos de ventas durante un periodo de tiempo largo.
Seleccionar los parámetros.
Calcular el pronóstico.
Monitorear y actualizar.
La técnica de suavizamiento exponencial doble se usa para pronosticar series de tiempo que tienen tendencia lineal.
